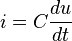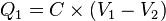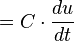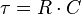électronique difusion - Condensateur

Condensateurs électrochimiques (électrolytiques aluminium). Le 1^er est de1 000 µF pour une tension de service de35 V (modèle axial), le 2^e est de 10 µF pour160 V (modèle radial).

Un condensateur est un composant électronique ou électrique élémentaire, constitué de deux armatures conductrices (appelées « électrodes ») en influence totale et séparées par un isolant polarisable (ou « diélectrique »). Sa propriété principale est de pouvoir stocker des charges électriques opposées sur ses armatures. La valeur absolue de ces charges est proportionnelle à la valeur absolue de la tension qui lui est appliquée. Le condensateur est caractérisé par le coefficient de proportionnalité entre charge et tension appelé capacité électrique et exprimée en farads (F). La relation caractéristique d'un condensateur idéal est :

$i = C{duover dt}$

où :

i est l'intensité du courant qui traverse le composant, exprimée en ampère (symbole A) ;
u est la tension aux bornes du composant, exprimée en volt (symbole V) ;
C est la capacité électrique du condensateur, exprimée en farad (symbole F).
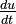$textstyle{{duover dt}}$ est la dérivée de la tension par rapport au temps.

Les signes sont tels que l'électrode par laquelle entre le courant (dans le sens conventionnel du courant) voit son potentiel augmenter.

Le condensateur est utilisé principalement pour :

stabiliser une alimentation électrique (il se décharge lors des chutes de tension et se charge lors des pics de tension) ;
traiter des signaux périodiques (filtrage…) ;
séparer le courant alternatif du courant continu, ce dernier étant bloqué par le condensateur ;
stocker de l'énergie, auquel cas on parle de supercondensateur.

Condensateurs électrochimiques (électrolytiques aluminium). Le 1^er est de1 000 µF pour une tension de service de35 V (modèle axial), le 2^e est de 10 µF pour160 V (modèle radial).

Loi de comportement du condensateur[modifier]

Article détaillé : Capacité électrique.

Symbole d'un condensateur non polarisé dans un circuit.

On définit la capacité par la relation :

$Q = Ctimes U$

où :

Q est la charge stockée sur sa borne positive et s'exprime en Coulombs;
U est la tension aux bornes du composant ;
C est la capacité électrique du condensateur.

Expression algébrique de la loi de comportement du condensateur :

$textstyle{Q_1 = Ctimes (V_1-V_2)}$

Les indices 1 et 2 repérant chacune des bornes. Q_k étant la charge de la borne k et V_k son potentiel électrique (k = 1 ou 2). La borne au potentiel le plus élevé (borne positive) est donc chargée positivement. La charge « totale » d'un condensateur Q_t = Q₁ + Q₂ est donc nulle. Procédant par influence électrostatique, le courant « pénétrant » par une borne ressort à l'identique par l'autre borne, bien que les armatures soient séparées par un isolant.

Si l'on oriente la branche de circuit contenant le condensateur dans le sens : borne 1 → borne 2, fixant ainsi le sens positif du courant i, on définit alors algébriquement la tension u dans le sens opposé (convention récepteur)

u = V 1 - V 2

Il devient alors possible de définir algébriquement une relation entre le courant circulant dans la branche et la dérivée temporelle de la tension :

$i= frac{dQ_1}{dt} ,$ $= C cdot frac{du}{dt} ,$

La valeur de la tension aux bornes du condensateur en régime transitoire en fonction du temps pour un système du premier ordre est définie par la relation suivante:

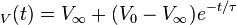$_ V(t)=V_{infty} +(V_0 - V_{infty} )e^{-t/tau}$ ,

V 0

est la tension initiale et 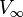$V_{infty}$ est la tension en régime permanent

et $τ$ est la constante de temps qui équivaut à

$tau = R cdot C$

dans un circuit ayant un condensateur en série avec une résistance. En connaissant les valeurs de tension initiales et finales, on peut en déduire le temps $t$ .

Composant électrique ou électronique[modifier]

Plusieurs types de condensateurs. De gauche à droite : céramique multicouche, céramique disque, film polyester multicouche, céramique tubulaire, polystyrène, film polyester métallisé, électrolytique aluminium. Unité de mesure en centimètres.

Le mot condensateur peut désigner spécifiquement un composant électrique ou électronique conçu pour pouvoir emmagasiner une charge électrique importante sous un faible volume ; il constitue ainsi un véritable accumulateur d'énergie.

En octobre 1745, Ewald Georg von Kleist de Poméranie inventa le premier condensateur. Le physicien hollandais Pieter van Musschenbroek le découvrit de façon indépendante en janvier 1746. Il l'appela la bouteille de Leyde car Musschenbroek travaillait à l'université de Leyde.

Un condensateur est constitué fondamentalement de deux conducteurs électriques, ou « armatures », très proches l'un de l'autre, mais séparés par unisolant, ou « diélectrique ».

La charge électrique emmagasinée par un condensateur est proportionnelle à la tension appliquée entre ses deux armatures. Aussi, un tel composant est-il principalement caractérisé par sa capacité, rapport entre sa charge et la tension.

La capacité électrique d'un condensateur se détermine essentiellement en fonction de la géométrie des armatures et de la nature du ou des isolants ; la formule simplifiée suivante est souvent utilisée pour estimer sa valeur :

$C = varepsilon {S over e}$

avec S : surface des armatures en regard, e distance entre les armatures et ε la permittivité du diélectrique.

L'unité de base de capacité électrique, le farad représente une capacité très élevée, rarement atteinte (à l'exception des supercondensateurs) ; ainsi, de très petits condensateurs peuvent avoir des capacités de l'ordre du picofarad.
Une des caractéristiques des condensateurs est leur tension de service limite, qui dépend de la nature et de l'épaisseur de l'isolant entrant dans leur constitution. Cet isolant présente une certaine rigidité diélectrique, c'est-à-dire une tension au-delà de laquelle il peut apparaître un violent courant de claquage qui entraîne une destruction du composant (sauf pour certains d'entre eux, dont l'isolant est dit auto-cicatrisant).

La recherche de la plus forte capacité pour les plus faibles volume et coût de fabrication conduit à réduire autant que possible l'épaisseur d'isolant entre les deux armatures ; comme la tension de claquage diminue également dans la même proportion, il y a souvent avantage à retenir les meilleurs isolants.

Désignation	Capacité	Champ électrique
Condensateur plan	$C = varepsilon_0varepsilon_mathrm{r} cdot frac{A}{d}$	$E = frac{Q}{varepsilon_0 varepsilon_mathrm{r} A}$
Condensateur cylindrique	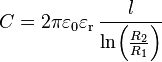$C=2pi varepsilon_0varepsilon_mathrm{r} , frac{l}{ln!left(frac{R_2}{R_1}right)}$	$E(r) = frac{Q}{2pi r l varepsilon_0 varepsilon_mathrm{r}}$
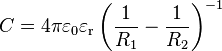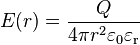Condensateur sphérique	$C=4 pi varepsilon_0 varepsilon_mathrm{r} left( frac{1}{R_1}-frac{1}{R_2}right)^{-1}$	$E(r) = frac{Q}{4pi r^2 varepsilon_0 varepsilon_mathrm{r}}$
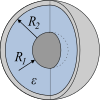Sphère	$C = 4πε 0 ε r R 1$	$E(r) = frac{Q}{4pi r^2 varepsilon_0 varepsilon_mathrm{r}}$

où $ε 0$ représente la permittivité relative du vide (8,84 10-12 Fm-1) et $ε r$ la permitivité relative de l'isolant.